확률변수가 가질 수 있는 값이 {1,2,3, ...} 와 같이 유한개이거나 무한 개의 셀 수 있는 값으로 표현될 수 있을 경우 이산형 확률변수라고 합니다. 예를 들어 가족 구성원의 수, 학과 학생들의 수, 동전 던지기에서 앞면이 나오는 횟수 등 실생활에서 접할 기회가 많습니다. 이산형 확률변수가 나올 수 있는 값의 범위에 대한 확률을 표현할 때 특정 함수를 쓰게 됩니다. 이 함수를 확률질량함수(probability mass function)라고 합니다. 또는 이산형 확률밀도함수라고도 합니다. 확률변수가 아래 조건을 만족하면 이산형 확률변수라고 합니다.
① 이산형 확률변수 X의 범위가 유한하거나 무한개의 셀 수 있는 값을 가지고 있다
ex) 가족 구성원의 수, 동전 던지기의 앞면이 나오는 횟수 등
② $\sum_{1}^{n} f(x_i) = 1$ : 이산형 확률변수 X의 확률을 모두 더하면 1이다
③ $f(x)\geq0$ : 모든 실수 $x$에 대해 $f(x)$는 0보다 크거나 같다
확률밀도함수(probability density function)이란 확률변수의 분포의 형태를 나타낼 때 사용합니다. 즉 확률밀도함수 $f(x)$가 주어졌을 때 $f(x)$는 그래프의 모양을 결정합니다.
예를 들어 아래 그림은 $f(x)=3x$의 그래프를 나타냅니다. 보는 바와 같이 $f(x)$가 그래프의 모양을 결정합니다.
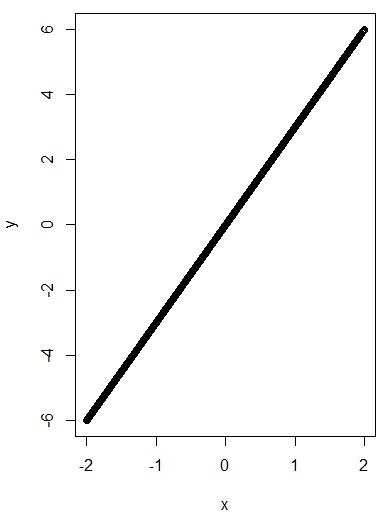
아래 그림은 정규분포의 그래프인데, 이 때 연속형 확률밀도함수 $f(x)$가 이같은 모양을 나타내기 때문입니다.
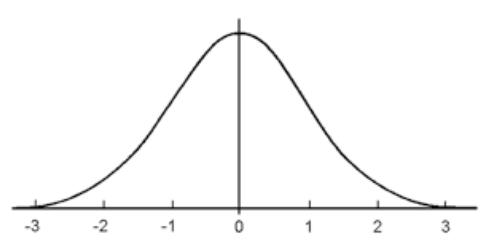
연속형 확률변수란 그 범위가 셀 수 없는 무한개일 때를 말합니다. 예를 들어 시간이나 몸무게 등을 말합니다. 이들을 셀 수 없을 뿐더러 그 범위가 무한입니다. 보통 편의상 시간은 '한 시간'이나 몸무게는 '65kg' 와 같이 말하고 있지만 그 뒤에 끝없는 소수점의 값들이 있습니다. 65.021753... kg 일 수도 있다는 거죠.
따라서 연속형 확률변수의 확률밀도함수 $f(x)$는 이산형과는 달리 특정 점에서의 확률이 0이기 때문에 확률은 구간을 적분하여 구할 수 있습니다. 연속형 확률밀도함수는 다음이 성립합니다.
① $f(x)\geq0$ : 모든 실수 $x$에 대해 $f(x)$는 0보다 크거나 같다
② $\int_{-\infty}^{\infty} f(x) dx=1$ : 확률밀도함수 $f(x)$를 전 구간에서 적분하면 1이 된다
③ $P(X=x)=0$ : 특정 점에서 확률이 0이다
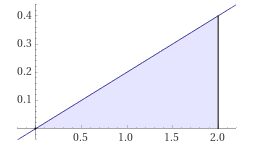
예제. 구간$[0,\sqrt{10}]$에 정의된 연속형 확률밀도함수 $f(x) = x/5$ 이다. $0<X<2$의 확률은 얼마인가?

'통계학개론' 카테고리의 다른 글
| [확률변수와 확률분포] 8. 누적분포함수(cumulative distribution function) (0) | 2021.02.14 |
|---|---|
| [확률변수와 확률분포] 6. 확률변수(random variable) (0) | 2021.02.12 |
| [확률론] 5. 베이즈 정리(Bayes' theorem) (0) | 2021.02.11 |
| [확률론] 4. 독립과 배반사건의 개념 (0) | 2021.02.11 |
| [확률론] 3. 조건부 확률의 정의 (0) | 2020.05.19 |