사건을 구분하는 것이 크게 어려운 개념은 아니지만 잘못하면 헷갈릴 수도 있는 개념들입니다.
1. 배반사건
두 사건 A, B가 있을 때 A∩B가 의미하는 바는 A사건과 B사건이 동시에 일어난다는 것이죠.
하지만 동시에 일어나는 사건이 아예 없으면 어떨까요?
예를 들면 주사위를 던지는데 A는 짝수가 나올 사건이고 B는 홀수가 나올 사건이라고 한다면 두 사건이 동시에 일어날 수 있을까요? 당연히 불가능하겠죠
이 때 A∩B= ø 이 성립합니다. 이를 "두 사건 A와 B는 상호배반적이다" 라고 합니다.
2. 독립
추론 통계에서 독립이라는 조건을 이해하는게 중요한데 많은 핵심 개념들이 독립을 전제로 하고 있기 때문입니다. 따라서 매우 중요한 개념이기 때문에 꼭 짚고 넘어가야할 부분입니다. 특히 배반사건과 독립을 구분하는데에 어려움을 겪는 분들이 있습니다. 물론 저도 처음 배울 땐 그랬고요.
이 전에 포스팅했던 조건부확률 P(A|B) 의 의미는 B사건이 일어날 때 A사건이 일어나는 확률입니다. 다시 말해서 위의 확률을 구하는 전제조건은 B사건이 A사건에 영향을 미친다는 것입니다. 그런데 B사건이 A에 영향을 끼치지 않는다면 어떨까요? 지난번에 쓴 예제를 통해 살펴보겠습니다.
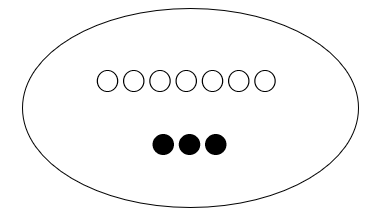
주머니 속에 검은공이 3개 하얀공이 7개 들어있다고 할 때 주머니 속에서 3개의 공을 꺼냅니다. 이 때 공을 꺼내는 건 세 번 꺼내야겠죠?
① 공을 꺼냅니다. 남은 공은 9개입니다.
② 공을 꺼냅니다. 남은 공은 8개입니다.
③ 공을 꺼냅니다. 남은 공은 7개입니다.
이와 같이 공을 하나씩 꺼낼 때마다 다음번에 공을 꺼내는 사건에 영향을 미칩니다.
그렇다면 공을 꺼내고 다시 넣은 다음에 또 다시 공을 꺼내는 건 어떨까요? 즉, 복원추출을 합니다. 이전에 공을 꺼낸 사건이 다음에 뽑는 사건에 영향을 끼치지 않습니다. 물론 다시 넣으면서 공의 배치가 달라져서 bias가 일어날 수도 있겠지만 그런 부분까지는 고려하지 않도록 하죠.
이제 배반사건과 구분하는건 크게 어렵지 않을 겁니다. A∩B= ø 이 배반사건이었죠. 독립은 동시에 일어날 수 있지만 서로 영향을 끼치지 않다는 거죠. 따라서 조건부확률 P(A|B)은 B가 A에 영향을 끼치지 않으면 P(A)와 같기 때문에 P(A|B)=P(A)로 다시 쓸 수 있습니다. 두 사건 A와 B가 독립일 때 동시에 일어나는 확률은 P(A), P(B) 곱으로 나타낼 수 있는데 다음과 같습니다.
P(A∩B) = P(A|B)*P(B) = P(A)*P(B)
독립을 가정하면 많은 통계 개념이 단순화됩니다. 상식적으로 서로 영향을 끼치는 것까지 고려하면 계산이 매우 복잡해질 겁니다. 수학적으로도 어려워 질 것이구요..!
'통계학개론' 카테고리의 다른 글
| [확률변수와 확률분포] 6. 확률변수(random variable) (0) | 2021.02.12 |
|---|---|
| [확률론] 5. 베이즈 정리(Bayes' theorem) (0) | 2021.02.11 |
| [확률론] 3. 조건부 확률의 정의 (0) | 2020.05.19 |
| [확률론] 2. 확률의 정의 (0) | 2020.05.13 |
| [확률론] 1. 표본공간과 사건 (0) | 2020.05.11 |