조건부 확률(Conditional probability)이란 어떤 사건이 일어났다는 전제 하에 다른 사건이 일어날 확률입니다.
두 사건 A, B가 있을 때, 사건 A가 일어났을 때 B가 일어날 확률은 다음과 같이 표현합니다.


위 밴다이어그램을 보면 쉽게 이해할 수 있습니다. P(B|A)는 A에 대한 A∩B의 확률인 것을 알 수 있습니다.
만약 한 개의 주사위를 던질 때 짝수가 나오는 사건을 A라고 하고, 3의 배수가 나오는 사건을 B라고 했을 때 P(B|A)는 다음과 같습니다.

조건부 확률의 정의로부터 A와 B가 동시에 일어날 확률 P(A∩B)를 다음과 같이 유도할 수 있습니다.
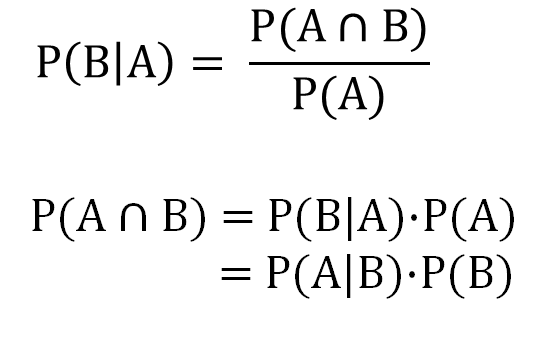
즉, A와 B가 동시에 일어날 확률은 A의 확률과 A가 일어났다는 전제하에 B의 확률을 곱한 것과 같습니다.
예를 들어, 주머니 속에 검은공이 3개 하얀공이 7개 들어있다고 할 때 주머니 속에서 3개의 공을 꺼냅니다. 이 때 3개의 공이 모두 검은공일 확률을 구해보겠습니다. 첫 번째 공을 꺼내는 사건을 A, 두 번째 공을 꺼내는 사건을 B, 세 번째 공을 꺼내는 사건을 C라고 한다면,
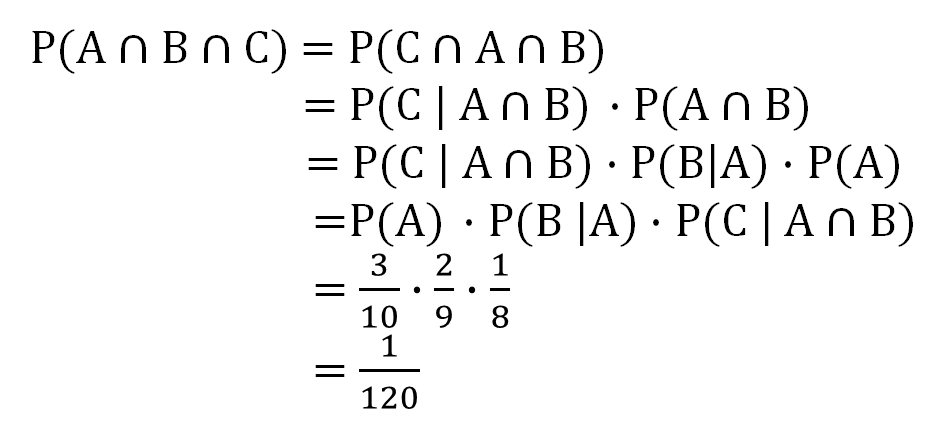
10개 중 검은 공 3개 중 하나를 꺼내는 확률을 3/10, 남은 공 9개 중 검은 공 2개 중 하나를 꺼내는 확률을 2/9, 남은 공 8개 중 검은공 1개를 꺼내는 확률은 1/8입니다. 이들을 모두 곱하면 같은 답이 나옵니다. 이렇게 직관적으로 확률을 구할 수 있지만 조건부 확률에 대한 원리가 있음을 기억해 두면 좋겠습니다.
위의 결과를 일반화하면 k개의 사건에 대한 교집합의 확률은 다음의 식으로 나타낼 수 있습니다.
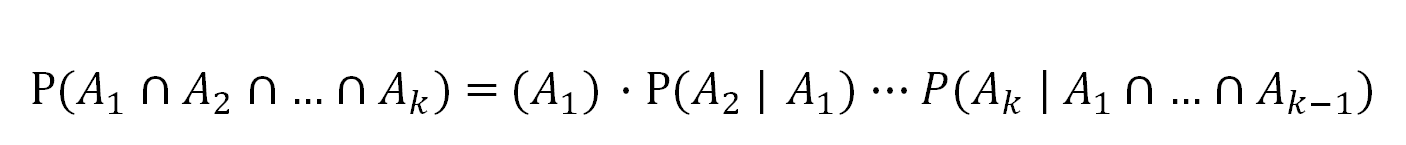
'통계학개론' 카테고리의 다른 글
| [확률변수와 확률분포] 6. 확률변수(random variable) (0) | 2021.02.12 |
|---|---|
| [확률론] 5. 베이즈 정리(Bayes' theorem) (0) | 2021.02.11 |
| [확률론] 4. 독립과 배반사건의 개념 (0) | 2021.02.11 |
| [확률론] 2. 확률의 정의 (0) | 2020.05.13 |
| [확률론] 1. 표본공간과 사건 (0) | 2020.05.11 |